もう少し進んだ電気理論の話(抵抗の合成)
こんにちは.
以前このブログで1回だけ電気理論の話をしたことがありますが,その時は本当に基本だけのお話でした.
いわば,以下のような最高に単純な回路のみ扱えるような理論です.
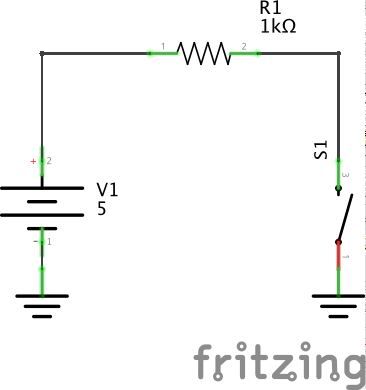
この時の電流は,
V = RIより,
I = V/Rなので,
5/1,000 = 5mA
のように計算することが出来ました.
では,下記のような場合はどうでしょう.

抵抗を水車,電流を水流と見立てると,水流を妨げる力は2個の水車の合計になることが想像できます.これは電気にも当てはまるため,回路中の合計の抵抗値Rは下記の式で表されます.
R = R1 + R2
つまり,回路に流れる電流Iは,
I = V/R = V/(R1+R2)
5V/(1,000 + 500) = 約3.3 mA
では下記のような場合はどうでしょうか.

この場合も水路に例えて考えましょう.水路が分岐していますが,分かれる前と別れた後の水流の合計は変わらないはずです.これは電気の場合も同じです.このため,分岐前の電流Iは以下の式で表すことが出来ます.
I = I1 + I2
ただし,I1: R1を流れる電流 I2 = R2を流れる電流
この時,R1とR2の前後にかかる電圧はどちらも等しくなります.なぜなら,各抵抗のすぐ手前の電圧は分岐直前の電圧(電源電圧)に等しく,各抵抗のすぐ後ろの電圧は合流直後の電圧と同じためです.これを踏まえて考えると,
I = I1 + I2
V= V1 = V2
I1 = V/R1, I2 = V/R2より,
V/R1 + V/R2 = I
V(1/R1+1/R2) = I
I/V = 1/R1 + 1/R2
ここで,R = V/Iなので,
1/R = I/V = 1/R1 + 1/R2 よって,
1/R = 1/R1 + 1/R2
となります.ちょっと長いですが,要はR1とR2を足すには,1をそれぞれの抵抗値で割って(1/R1と1/R2),それらを足して(1/R1 + 1/R2),その数字で1を割れば出ます,ということですね.
これで複数の抵抗が1個の回路に含まれる場合の計算ができるようになりました.これで扱える回路が一気に増えましたね.
参考文献
特になし.